Problem 3

Run Bertini to find all the complex solutions of

\[x^5 + y+1 \,\,= \,\, y^5 + z + 1 \,\,= \,\, z^5 + x + 1 \quad = \quad 0 .\]

How many are real? Now, solve the same system using Singular.

Solution

In Macaulay 2:

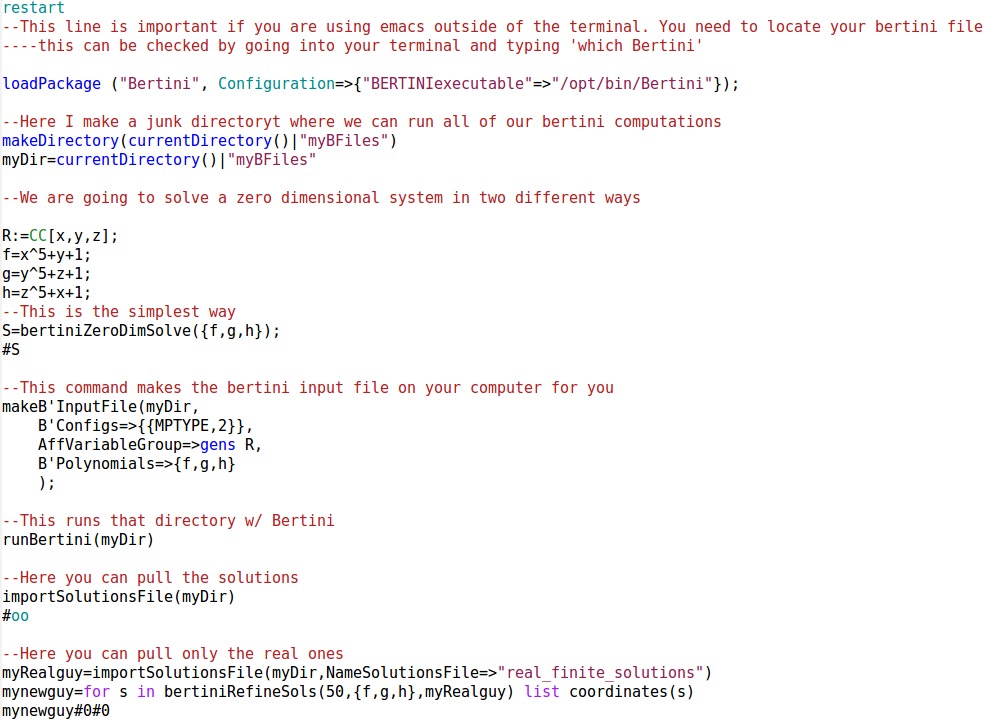
--This line is important if you are using emacs outside of the terminal. You need to locate your bertini file
----this can be checked by going into your terminal and typing 'which Bertini'

loadPackage ("Bertini", Configuration=>{"BERTINIexecutable"=>"/opt/bin/Bertini"});

--Here I make a junk directoryt where we can run all of our bertini computations
makeDirectory(currentDirectory()|"myBFiles")
myDir=currentDirectory()|"myBFiles"

--We are going to solve a zero dimensional system in two different ways

R:=CC[x,y,z];
f=x^5+y+1;
g=y^5+z+1;
h=z^5+x+1;
--This is the simplest way
S=bertiniZeroDimSolve({f,g,h});
#S

--This command makes the bertini input file on your computer for you
makeB'InputFile( myDir,
                 B'Configs=>{{MPTYPE,2}},
                 AffVariableGroup=>gens R,
                 B'Polynomials=>{f,g,h} );
--This runs that directory w/ Bertini
runBertini(myDir)
--Here you can pull the solutions
importSolutionsFile(myDir)
#oo
--Here you can pull only the real ones
myRealguy=importSolutionsFile(myDir,NameSolutionsFile=>"real_finite_solutions")
mynewguy=for s in bertiniRefineSols(50,{f,g,h},myRealguy) list coordinates(s)
mynewguy#0#0

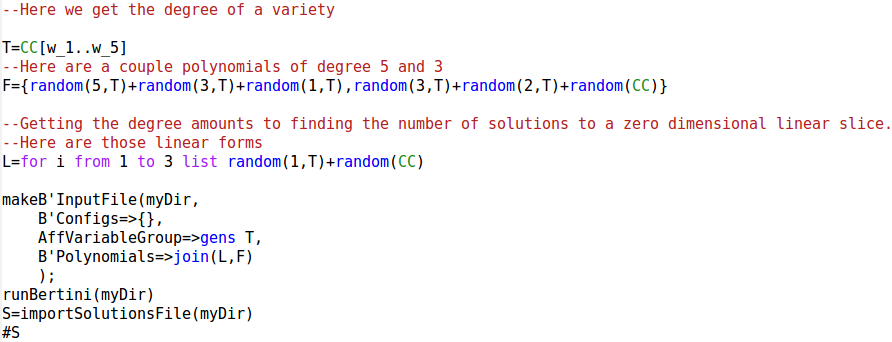
--Here we get the degree of a variety

T=CC[w_1..w_5]
--Here are a couple polynomials of degree 5 and 3
F={random(5,T)+random(3,T)+random(1,T),random(3,T)+random(2,T)+random(CC)}
--Getting the degree amounts to finding the number of solutions to a zero dimensional linear slice.
--Here are those linear forms
L=for i from 1 to 3 list random(1,T)+random(CC)

makeB'InputFile( myDir,
                 B'Configs=>{},
                 AffVariableGroup=>gens T,
                 B'Polynomials=>join(L,F) );
runBertini(myDir)
S=importSolutionsFile(myDir)
#S

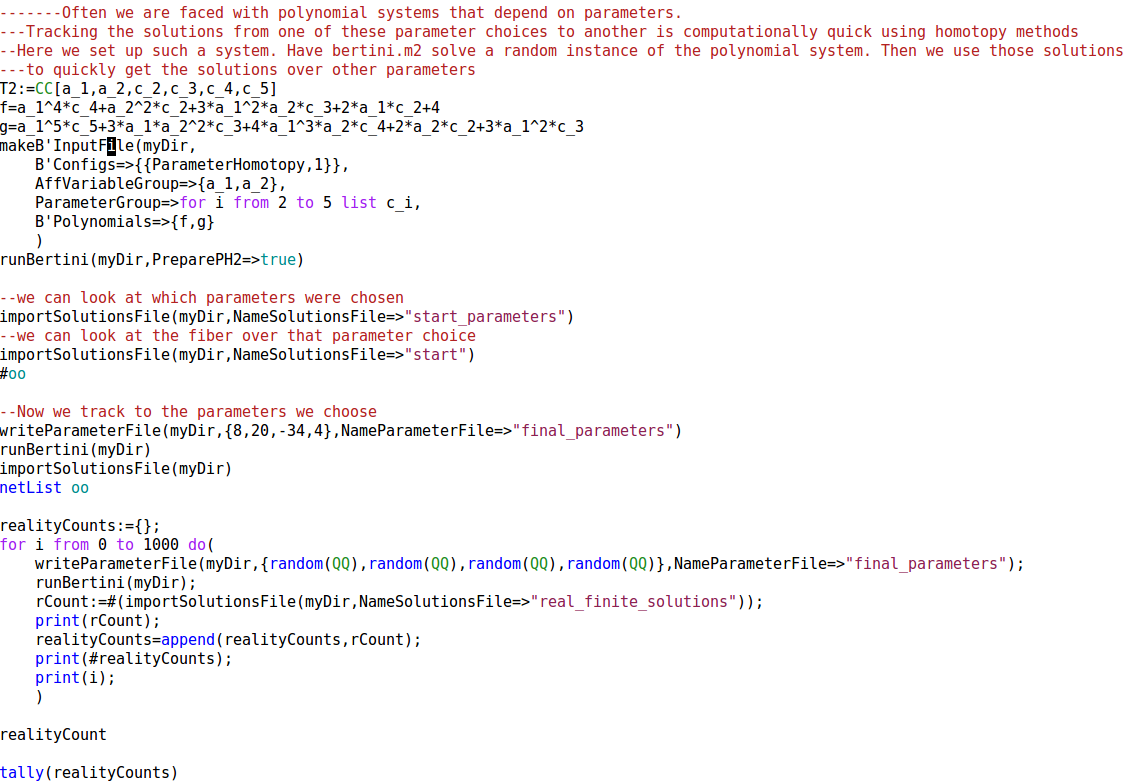
-------Often we are faced with polynomial systems that depend on parameters.
---Tracking the solutions from one of these parameter choices to another is computationally quick using homotopy methods
--Here we set up such a system. Have bertini.m2 solve a random instance of the polynomial system. Then we use those solutions
---to quickly get the solutions over other parameters
T2:=CC[a_1,a_2,c_2,c_3,c_4,c_5]
f=a_1^4*c_4+a_2^2*c_2+3*a_1^2*a_2*c_3+2*a_1*c_2+4
g=a_1^5*c_5+3*a_1*a_2^2*c_3+4*a_1^3*a_2*c_4+2*a_2*c_2+3*a_1^2*c_3
makeB'InputFile( myDir,
                 B'Configs=>{{ParameterHomotopy,1}},
                 AffVariableGroup=>{a_1,a_2},
                 ParameterGroup=>for i from 2 to 5 list c_i,
                 B'Polynomials=>{f,g})
runBertini(myDir,PreparePH2=>true)

--we can look at which parameters were chosen
importSolutionsFile(myDir,NameSolutionsFile=>"start_parameters")
--we can look at the fiber over that parameter choice
importSolutionsFile(myDir,NameSolutionsFile=>"start")
#oo

--Now we track to the parameters we choose
writeParameterFile(myDir,{8,20,-34,4},NameParameterFile=>"final_parameters")
runBertini(myDir)
importSolutionsFile(myDir)
netList oo

realityCounts:={};
for i from 0 to 1000 do(
    writeParameterFile(myDir,{random(QQ),random(QQ),random(QQ),random(QQ)},NameParameterFile=>"final_parameters");
    runBertini(myDir);
    rCount:=#(importSolutionsFile(myDir,NameSolutionsFile=>"real_finite_solutions"));
    print(rCount);
    realityCounts=append(realityCounts,rCount);
    print(#realityCounts);
    print(i);
)

realityCount

tally(realityCounts)

We can also solve it using Mathematica (Second input is computing that how long the process takes in second):

NSolve[{x^5 + y + 1, y^5 + z + 1, z^5 + x + 1} == 0];

Length[NSolve[{x^5 + y + 1, y^5 + z + 1, z^5 + x + 1} == 0, Reals]]

Timing[Length[NSolve[{x^5 + y + 1, y^5 + z + 1, z^5 + x + 1} == 0, Reals]]][[1]]